First of all, many thanks to Celandro for asking me to write about lucky Pokémon after reading my post on The Silph Road subreddit. This is a more refined article based on said post, reflecting on the questions and criticism of fellow players as well as some aspects I didn’t fully consider on my first analysis.
In this article we will explore the benefits of lucky Pokémon from an efficiency standpoint. To be precise, we want to find out when a lucky Pokémon has the same battle performance as a non-lucky Pokémon.
Introduction
As the reader is surely aware of, Lucky Pokémon are a new addition to the special Pokémon with the characteristic of reducing in half the stardust cost per power up. This means the total amount of stardust spent is also halved, introducing an appealing mechanism to obtain cheap, high IV (it has been found that floor value is 10) Pokémon. It can also be pretty much controlled taking into account older specimen yield a much higher probability of a Lucky trade, which makes this the most user-controlled mechanism we’ve ever had in the game.
That being said, there are still cases where lucky Pokémon might not the best option for powering up, as this analysis will try to discover under which circumstances this is the case. To be more precise, the following topics will be explored:
- Stardust optimization to reach a certain breakpoint in the best case scenario (15ATK IV) and worst case scenario (10ATK IV).
- Stardust startup cost due to fixed cost per trade and lucky probability.
- Increased requirements in candy to take advantage of lucky Pokémon stardust discount.
- The specific case of lucky legendaries.
For this analysis, the cumulative stardust and discrete stardust cost [1] has been used to compare the progression of lucky and non-lucky (we’ll call them normal from now on) Pokémon. Breakpoints have also been part of the study using u/dondon151 spreadsheet [2] while bulk points have been avoided to simplify the analysis since they are not so widespread or relevant as breakpoints.
Results and Discussion
Stardust Optimization and Breakpoints
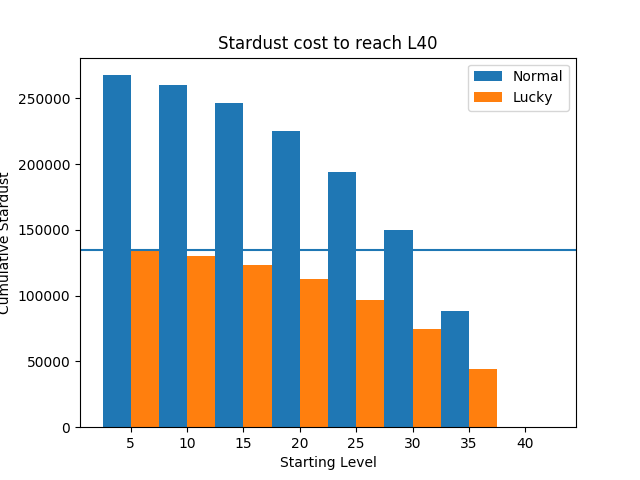
If we represent the stardust spent on a lucky and a normal Pokémon to reach level 40 (L40) as in figure 1, one can quickly see that the lowest level lucky Pokémon is cheaper than a L30 and below normal Pokémon.
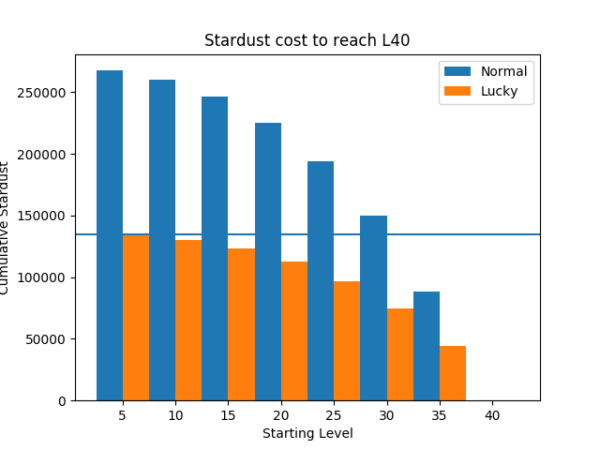
Figure 1. Cumulative stardust spent to reach level 40 from different starting levels for a normal (non-lucky) and lucky Pokémon at steps of 5 levels each.
However, there is no need to reach the level 40 if what we are looking for is to spend less stardust by reaching a certain breakpoint. While a similar bar representation to figure 1 could be extended to other max levels, a different kind of representation has been used in order to obtain a better understanding of the nature of the lucky stardust discount.
In figure 2 below we can see a function of a normal Pokémon level to reach a certain goal level (in this case, L36) with respect to a lucky Pokémon when they spend approximately the same amount of stardust to reach said level. The nature of power-ups makes this a step function, however, we will use a fitted function in order to simplify the analysis.
Since there is no analytical expression for this, a minimization method has been used where for a lucky Pokémon of level X we calculate the corresponding level Y of a normal Pokémon that spends almost the same amount of stardust to reach the same goal level. The expression that needs to be minimized is:
f(i,j,k) = |Cn(j,k) – Cl(i,k)|
where Cn(j,k) is the cumulative stardust cost for a normal Pokémon to go from level j to level k, Cl(i,k)=Cn(i,k)/2 is the same but for a lucky Pokémon starting at level j and i<j<k. Notice that i and k have to be fixed for each case to minimize the function.
Thus, we can rearrange the expression to be:
g(j) = |Cn(i,k)/Cn(j,k) – 2|
We minimize this function to obtain the level j at which a normal Pokémon matches the stardust spent by a lucky Pokémon of level i.
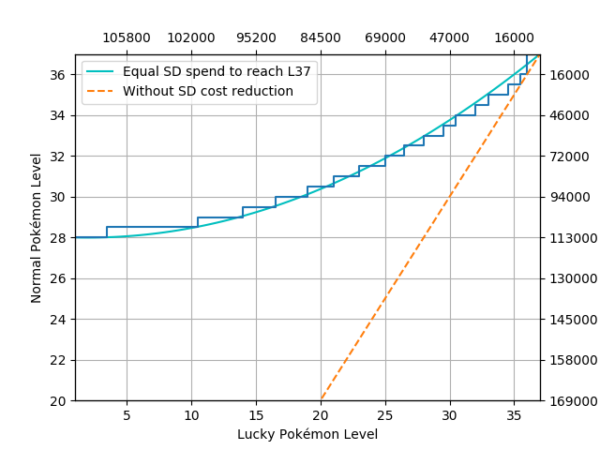
Figure 2. Normal Pokémon base level (Y-Axis) against lucky Pokémon base level (X-Axis) when at some point they spend approximately the same amount of stardust to reach level 37. The step function is the real data while the smooth function is a polynomial of order 2. The dashed line is the same representation if lucky Pokémon didn’t have the 50% stardust discount, added for reference. In front of each axis the cumulative stardust spent for each type of Pokémon is displayed.
As we can see in this example, when aiming at level 37, any lucky Pokémon of any level is cheaper than any normal Pokémon at level 28 or below. If we look at normal Pokémon at level 30, any lucky Pokémon at level 20 or above is cheaper than said normal specimen. We will refer to this curve as the discount boundary, any normal Pokémon above the curve is more stardust efficient than a lucky of the corresponding level or below and vice-versa. With this kind of graph we can distinguish the lower limit which will be considered as the minimum level of a normal specimen to be less efficient than a lucky specimen at any level.
In figure 3-6 we can see different goal levels evaluated on the same way were we find very similar results in the lower limit:
-
Aiming at L20: L14
-
Aiming at L30: L22
-
Aiming at L35: L26.5
-
Aiming at L40: L31
Thus it is safe to say that any normal Pokémon below level 20 is less stardust efficient than any lucky Pokémon with the same IVs. Since usually breakpoints are located in the upper 30s, one can assume that this lower limit can be safely raised to L25. This makes any egg and raid boss (weather boosted or not) Pokémon suboptimal in comparison with a lucky Pokémon of the same ATK IV, independent of level.
Other levels for normal Pokémon we should review are 30 (max for non-weather boosted) and 35 (weather boosted). Since this doesn’t fall in absolute limits, we need to look at each goal level specifically. In the case of level 30, we need to check figures 6 and 7 to notice that lucky specimens with levels 25 and above are always more efficient than their normal level 30 or below counterparts. For level 35, if we look at figure 2 the same happens to lucky Pokémon of level 32 and above.
This means that if we have a normal Pokémon of L30, we would want a L25 or higher lucky Pokémon. If our normal Pokémon were L35, then L32 or higher.
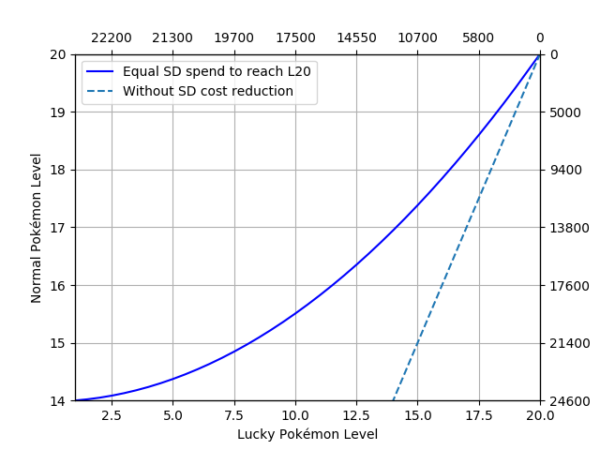
Figure 3. Normal Pokémon base level (Y-Axis) against lucky Pokémon base level (X-Axis) when at some point they spend approximately the same amount of stardust to reach level 20. The dashed line is the same representation if lucky Pokémon didn’t have the 50% stardust discount, added for reference. In front of each axis, the cumulative stardust spent on each type of Pokémon is displayed.
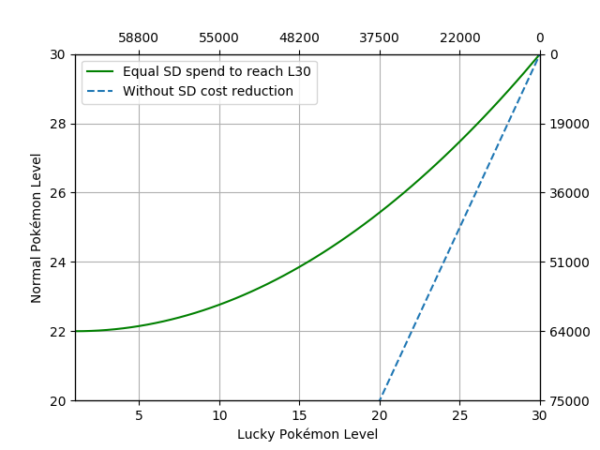
Figure 4. Normal Pokémon base level (Y-Axis) against lucky Pokémon base level (X-Axis) when at some point they spend approximately the same amount of stardust to reach level 30. The dashed line is the same representation if lucky Pokémon didn’t have the 50% stardust discount, added for reference. In front of each axis, the cumulative stardust spent on each type of Pokémon is displayed.
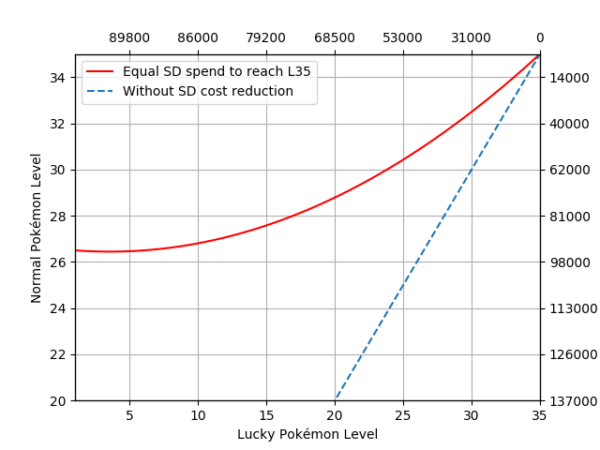
Figure 5. Normal Pokémon base level (Y-Axis) against lucky Pokémon base level (X-Axis) when at some point they spend approximately the same amount of stardust to reach level 35. The dashed line is the same representation if lucky Pokémon didn’t have the 50% stardust discount, added for reference. In front of each axis, the cumulative stardust spent on each type of Pokémon is displayed.
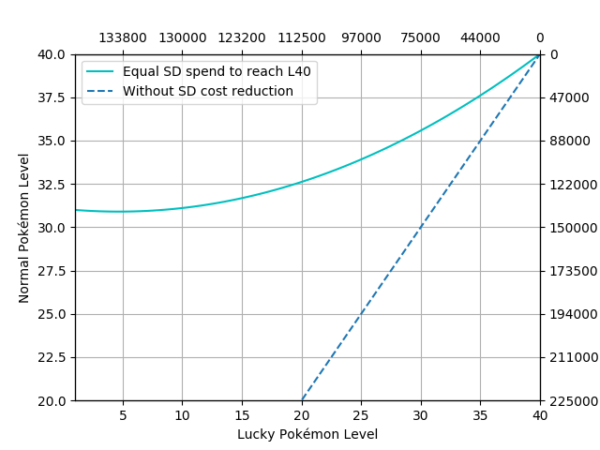
Figure 6. Normal Pokémon base level (Y-Axis) against lucky Pokémon base level (X-Axis) when at some point they spend approximately the same amount of stardust to reach level 40. The dashed line is the same representation if lucky Pokémon didn’t have the 50% stardust discount, added for reference. In front of each axis, the cumulative stardust spent on each type of Pokémon is displayed.
All the previous results give us a lower limit for L25 normal Pokémon and below, which corresponds to the best case scenario (only applicable if both the normal and lucky Pokémon hit the breakpoint at the same level because they have the same ATK IV). However, how do they compare in the worst case scenario? Now we compare 15 ATK IV normal Pokémon to their lucky counterparts with 10 ATK IV (the floor value for lucky Pokémon) to obtain the upper limit in the worst case scenario. Obviously, in the best case scenario were the lucky Pokémon has 15ATK IV there would be no upper limit as they would always hit the breakpoint with less or equal stardust spent.
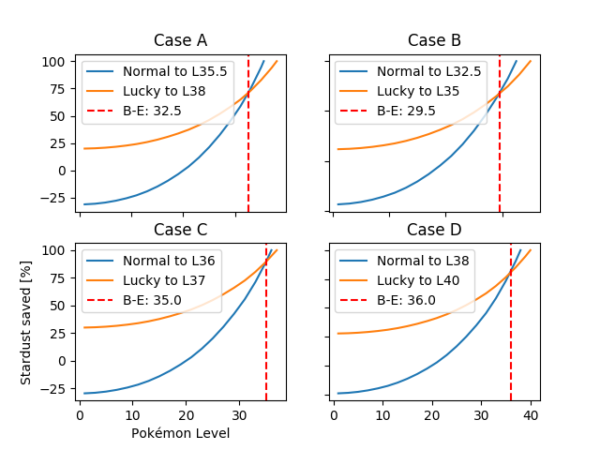
Figure 7. Percentage of stardust saved with respect to reference stardust cost with respect to Pokémon starting level for a normal Pokémon with 15ATK IV and a lucky Pokémon with 10ATK IV. The reference stardust cost is in each case the cost for a normal Pokémon from level 20 to the corresponding breakpoint level (L35.5 for case A, L32.5 for case B, L36 for case C and L38 for case D).
In figure 7 some real case breakpoints have been taken into account under different circumstances to obtain a realistic survey of practical cases. The match-ups studied to obtain these breakpoints were Machamp-Tyranitar (A), Raikou-Kyogre (B), Tyranitar-Moltres (C) and Raquaza-Rayquaza (D) with different weathers and friendship levels. This way we can extrapolate the obtained results to a general and easy to remember rule. As one can observe in the different graphs, the savings are always higher for the lucky Pokémon when comparing to a <L25 normal Pokémon, which is the same result for the lower limit obtained in the best case scenario. For the upper limit, we look at the break-even point from where normal Pokémon start being more stardust efficient than their counterparts. This point won’t be reached until L29.5 (case B) to L36 (case D).
With this we can make three simple checks to power up or not a lucky Pokémon:
-
Do you have a <L25 normal Pokémon with 15ATK IV? Any lucky Pokémon independently of its IVs will be more efficient
-
Do you have a >L25 normal Pokémon with 15ATK IV? A lucky Pokémon of the same level or above independently of its IVs will be more efficient
-
Do you have a >L30 normal Pokémon with 15ATK IV? A lucky Pokémon can only be more efficient with good ATK IV.
In the case the lucky Pokémon has great ATK IV (15 or 14), there won’t be any case a normal Pokémon can be more stardust efficient unless it has already hit the breakpoint.
Please take into account that while figure 4 indicates a relative measure with respect to a base stardust spending (from level 20 to a certain level in this case), the break-even points where the stardust performance changes are independent of this quantity, only IVs.
Demonstration: If we call X the stardust spent by a non-lucky Pokémon from level L to the first breakpoint level, Y the stardust spent by a lucky Pokémon from level L to the second breakpoint level and C is an arbitrary reference stardust cost.
Savings A: (1-X(lvl)/C)*100
Savings B: (1-Y(lvl)/C)*100
When are these quantities equal?
(1-X(L)/C)*100 = (1-Y(L)/C)*100 <=> 1-X(L)/C = 1-Y(L)/C <=> X(L)/C = Y(L)/C <=> Y(L) = X(L)
Which is independent of C.
Startup costs and side effects
Due to the nature of trading and lucky Pokémon, one needs to perform a certain number of trades, which cost stardust, but in exchange gives the player candy of the species you are trading. Depending on the distance of the trade, more candy is held at the same cost. Lucky probability is also influenced by another factor: time. The older the Pokémon traded, the higher probability of a lucky trade. However, no rigorous study on the nature of this tuning has been done at the moment. Thus, we will take the liberty of using hypothetical probabilities based on anecdotal data proposed by different players [3] in order to obtain conclusions about the influence of the startup cost (stardust spent on trades until a lucky one is achieved) in the global investment.
We will take 3 different hypothetical values for the lucky probability: 5%, 10, 20%. We reflect the influence of this probability in the following table:
| Probability | Number of trials until success | Stardust cost | Stardust cost (if legendary) | Candy obtained (scenario 1) | Candy obtained (scenario 2) | Candy obtained (scenario 3) |
|---|---|---|---|---|---|---|
| 5% | 20 | 2000 | 32000 | 39 | 79 | 139 |
| 10% | 10 | 1000 | 16000 | 19 | 39 | 69 |
| 20% | 5 | 500 | 8000 | 9 | 19 | 34 |
In table 1 we use 1/p as the number of trials until success where p is the lucky probability [4]. Scenario 1 reflects the case where all the trades are performed with two catches <10km away (1 candy) from each other and all except the lucky one have been transferred for an extra candy. Scenario 2 reflects the same case but with >100km of distance between each other (3 candies + 1 transfer). Scenario 3 takes advantage of the current trading event and takes the maximum possible amount (6 candies+1 transfer).
As seen in table 1, the stardust spent to find a lucky Pokémon is negligible in comparison with the global investment. This fact is reflected in figure 8, where dashed lines indicate the small displacement of the discount boundary at different end levels for non-legendaries. For legendaries, the trading cost is different depending on the friendship level, but we assume at least ultra friends (1600) for the sake of simplicity and the fact that it wouldn’t be efficient to mass trade legendaries at any lower friendship level. This increased cost will be analyzed in the next subsection, but for now, we can certainly assume that for non-legendary Pokémon, startup cost can be ignored and in most cases is worth it just for the candies.
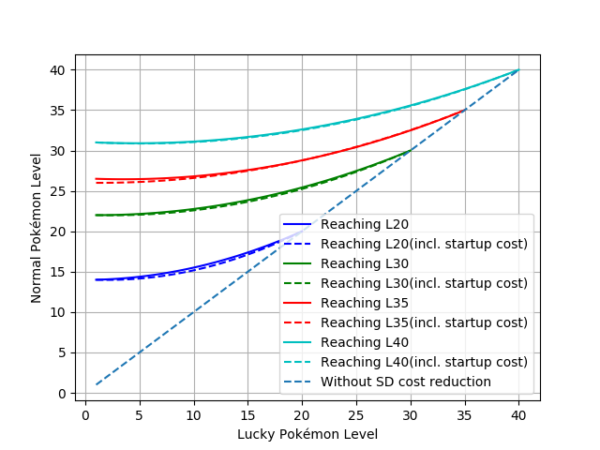
Figure 8. Normal Pokémon base level (Y-Axis) against lucky Pokémon base level (X-Axis) when at some point they spend approximately the same amount of stardust to reach a certain level. The dashed lines include the startup cost due to trading costs and a lucky probability of 5%.
Lucky Legendaries
In the case of legendary Pokémon, there are three important factors: trade cost, candy availability and level at catch. We will assume a fixed traded cost of 1600 stardust per trade, since that’s the cost for ultra friends and any lower level of friendship is inefficient for the sake of mass trading legendaries, as said before. Legendary and rare candy is way more scarce than candy of general species and even of pseudo-legendaries in most cases. This makes the argument of low-level lucky Pokémon as more efficient than higher level ones fall short at first glance. However, this can be compensated by the fact that legendaries are only obtainable at levels 15, 20 and 25. We will also assume only legendary-legendary trades for the sake of simplicity and efficiency in terms of stardust, not candy.
As discussed in previous sections, lucky Pokémon at any level are more stardust efficient than any normal Pokémon at level 25 or below. Since legendaries are only obtainable at level 25 or below, this might hold true if the startup cost for legendaries is not large enough to compensate the discount. Since we are only analyzing 3 different levels, we will change from the discount boundary representation to a typical stardust spent with respect to goal level graph.
In figure 9, the stardust cost increase due to the extra startup cost for a 5% lucky probability is indicated by arrows. Three different points must be highlighted. First, when L32 is the goal level, only L25 lucky specimens are more efficient than any other alternative. When the goal level is 34.5 the L20 lucky Pokémon are also more efficient than the rest. Lastly, when the goal level is L36 all lucky legendaries are more efficient than any normal counterpart. This means that if the lucky probability is indeed 5%, lucky legendaries of levels 25, 20 and 15 are only valuable for breakpoints above 32, 34.5 and 36 respectively. Please be aware that the only normal specimen that can be more efficient than the lucky ones is the weather boosted legendary, any other normal legendary will be less efficient than a lucky one, no matter the level of the latter.
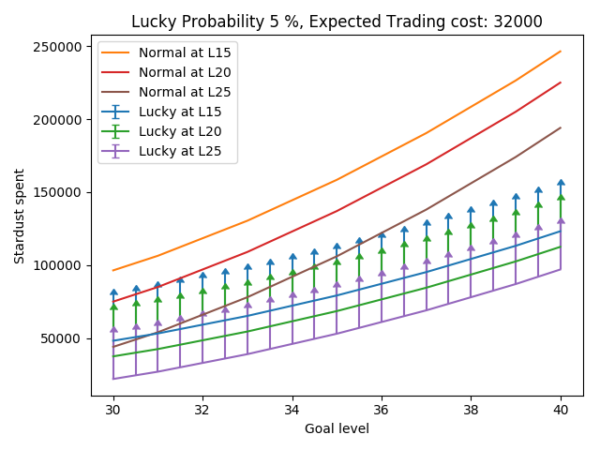
Figure 9. Stardust spent when reaching a certain goal level for a starting level for different cases. Lucky probability: 5%
However, if the lucky probability is 10%, these points are displaced to 30, 32.5 and 34 as shown in figure 11. Since in most cases the final breakpoint is on the upper 30s, if the lucky probability is 10% then lucky Pokémon are more efficient when they have the same ATK IV.
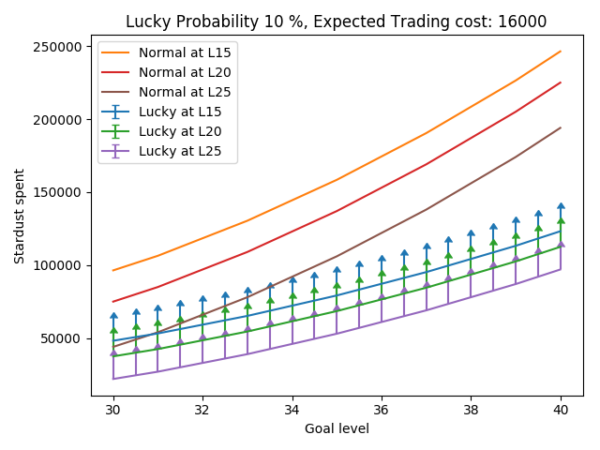
Figure 9. Stardust spent when reaching a certain goal level for a starting level for different cases. Lucky probability: 10%
As we have seen in a previously, this is the best case scenario since we are comparing the same IV specimens. To look at the worst case scenario we use the same example cases, taking into account the conditions imposed by legendary Pokémon. Figures 11 and 12 reflect the same cases we studied before but with this conditions into account. It can be seen in figure 11 that for a 5% lucky probability the L25 normal legendary can be equal or more efficient than a L25 lucky one on the more extreme cases (A and B) but in general, a 15ATK L25 normal legendary is as efficient as a 10ATK L15 lucky legendary.
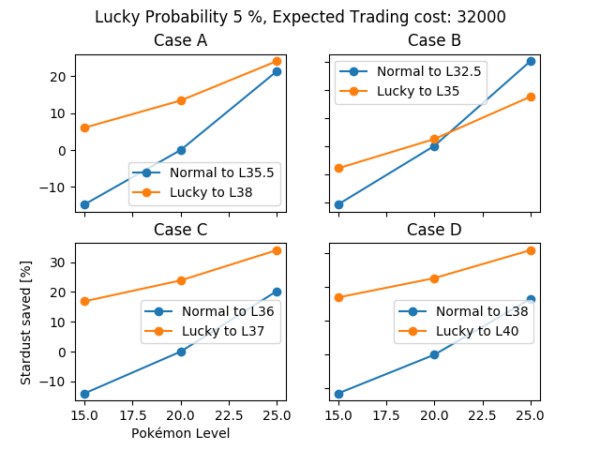
Figure 11. Stardust saved with respect to the cost from L20 to a certain goal level for different cases comparing lucky specimens with normal specimens. Lucky probability: 5%
If the lucky probability is 10% then a L25 normal legendary is as efficient as a L25 lucky one in the most extreme case but in general, it will be as efficient as a L15 lucky legendary, as seen in figure 12.
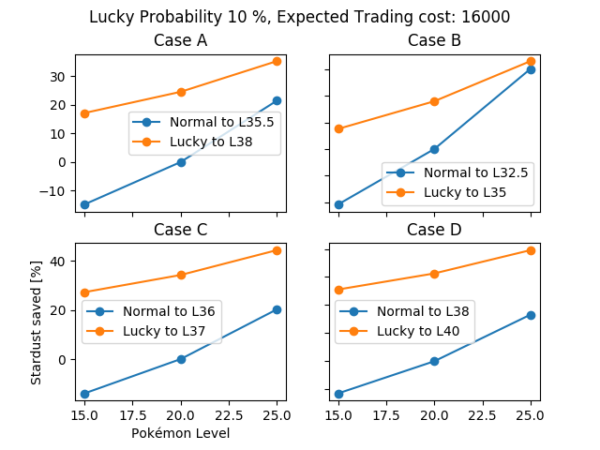
Figure 12. Stardust saved with respect to the cost from L20 to a certain goal level for different cases comparing lucky specimens with normal specimens. Lucky probability: 10%
Very similar results are obtained for a 20% probability, so it seems like trading L20 and above legendaries is the best way to obtain a usable lucky one if you have a 15 ATK L25 one to compete with.
How is this affected by the candy requirement as an overall optimization strategy? If we look at table 1 we can see that outside of the current trading event, if trades are performed as in scenario 1 (minimum candy possible) the player gets a total of 39 candies at 5% lucky probability, 19 at 10% and 9 at 5%. In contrast, the requirement is to go from level 15 to 25 is 48 candies, from level 15 to 20 is 20 candies and from level 20 to 25 is 28 candies.
Thus, if we assume 5% lucky probability, the player gets the necessary candies while trading to go from L15 to L20 and L20 to L25, only with an offset of 9 candies for the L15 to L25 gap. This makes the trading compensate level gap. In the case of a 10% probability, this is not the case and only compensates for the L15 to L20 case. Please be aware this is the worse case scenario. If the player has the chance to trade some legendaries during the present event or to trade with a friend whose legendaries are from +10km away, this compromise can be removed and candy will always surpass the level difference with any other option.
In any case, candy doesn’t seem to be the limiting factor for lucky legendaries, but the lucky probability and the breakpoint gap between 10 and 15 ATK IV.
Conclusions
The nature of lucky Pokémon has been studied to obtain rules to know when should one choose to power up a lucky specimen over a normal one.
In the case of non-legendaries, any lucky specimen is more stardust efficient than a <L25 (ATK IV doesn’t matter) or even <L30 (ATK IV matters). Even when weather boosted (L30 to L35) and with max ATK IV if the lucky specimen has great ATK IV (15-13), there is no contest, the lucky Pokémon is better.
Please keep in mind this is an important result. A lucky L1 specimen is more stardust efficient than a L25 perfect IV one you got from a weather boosted raid. Don’t hesitate to trade away low level Pokémon for the chance of getting a lucky one, even if they are low level! You will get enough candies from trading to compensate for the absence of candy discount.
In the case of legendaries, since the levels they can be obtained at is 15, 20 and 25, in most cases, any lucky legendary is more efficient than a nonweather boosted one and depending on the lucky probability and breakpoints, even weather boosted ones. So, to be on the safe side, try to trade L20 and L25 legendaries for the sake of efficiency.
[1] Power Up Costs, Gamepress, https://pokemongo.gamepress.gg/power-up-costs
[2] Raid breakpoint and bulkpoint tool, u/dondon151, https://docs.google.com/spreadsheets/d/1biaUoyriPgwS9sG4AbpOoyiZsnxBWzkm8xDPel4cGy4/edit#gid=0
[3] Getting Lucky: Results from trading 700 Pokémon this week, The Silph Road subreddit, https://www.reddit.com/r/TheSilphRoad/comments/94qeni/getting_lucky_results_from_trading_700_pok%C3%A9mon/
[4] Number of Trials to First Success, Cut the knot, https://www.cut-the-knot.org/Probability/LengthToFirstSuccess.shtml

nobody is maxing out pokemon just because it costs less star dust. at 40 you gonna max anything you touch. i don’t care if I spend 250 or 300k dust. it will be the best specimen i can reasonably get. why max something just because it is cheaper?
This analysis is not for the sake of choosing what to get to L40 no matter what. This serves as a guide to choose what to power up if you are looking for breakpoints instead of just maxing out whatever you want to. I understand there are players who don’t care about breakpoints and resource efficiency, this is for the rest of the playerbase (including some 40s as myself).
But to reply to your last question. You want to optimize your resources when:
A. You don’t have the resources to max out a number of the same species for raids or gyms
B. You don’t want to spend stardust on species you are going to use once for a challenge (see Venomoth for example)
C. You don’t care about maxing out, just breakpoints because you hoard resources in case an exclusive move pops up in the future and you can loose most of your resources before that
This is really good, high level reading. Well written and thank you for doing it. One takeaway that I knew once, but had forgotten was the general assumption/knowledge that the older a pokemon being traded, the more likely it is to go lucky.
I was not aware this was “fact.” Obviously there is the “first ten traded of a certain age” automatically going lucky, which I – and probably a lot of others – totally BLEW because I didn’t know enough about the game when it happened and had no idea what was happening and now I have a lot of very low level, cruddy pokemons that were automatic lucky trades and I did not know. 🙁
But I wasn’t aware this was an actual known thing. Since this was written some time ago, I am going to see if anyone has done more research on that.
Thank you for writing this! It is outstanding.