Catch probability

A Pokémon’s catch probability depends on several factors such as throw bonuses, the Pokémon’s Level, and ball and berry choices (see Table 9). Each Pokémon also has an individual base catch rate (BCR), so some are harder to catch than others.

Warning: The following sections about consecutive catch probabilities and expectation values are a bit more math heavy. They are meant for people, who want to know how, lucky they were with their catches. If you don’t want to dive deeply into it, I recommend sticking with the graphs and summaries below them.

The catch rate is given by:

CPM is a value dependent on the Pokémon’s level (Source). This is especially important since weather boosted raid bosses now must be caught at level 25 instead of 20. A good analysis on the effect of the weather boost on catch rates can be found here (link).

Bonus	Factor
Golden Razz Berry	2.5
Razz Berry	1.5
Curve ball	1.7
Throw bonus	2-Radius,       Radius
Pokéball or Premier Ball	1.0
Great Ball	1.5
Ultra Ball	2.0
Bronze medal for catching Pokémon of the same type	1.1
Silver medal	1.2
Gold medal	1.3

Table 9: Multipliers increasing the catch chance (Source)

Examples for base catch rates:

• Suicune, Raikou, Entei, Lugia, Ho-Oh: 2 %
• Articuno, Zapdos, Moltres: 3 %
• Level 4 raid bosses: 5 %
• Mewtwo: 6 %

To understand visually:

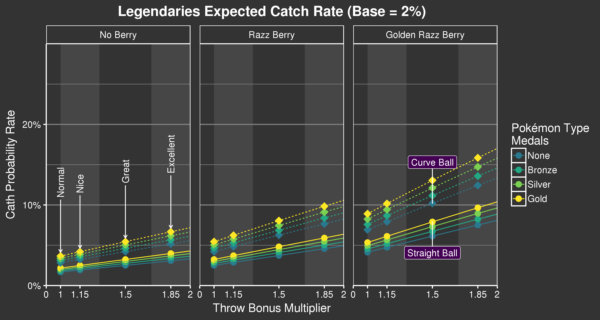
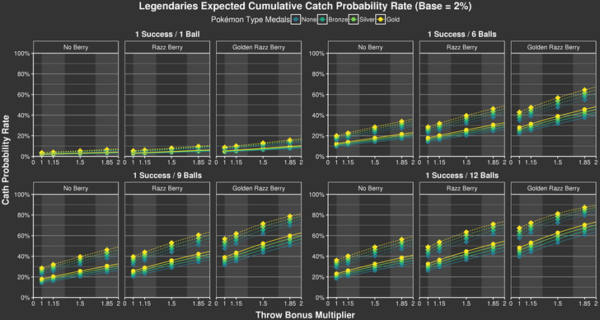
Figure 1: Combined catch probability for Pokémon with a BCR of 2 % (Source)

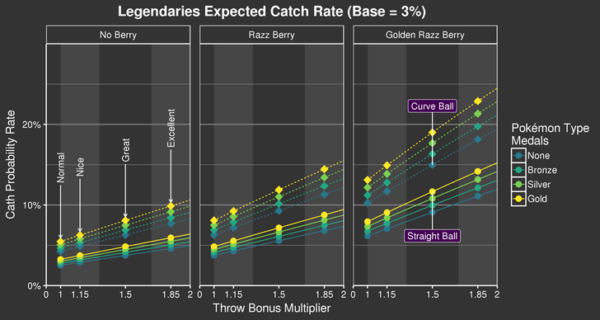
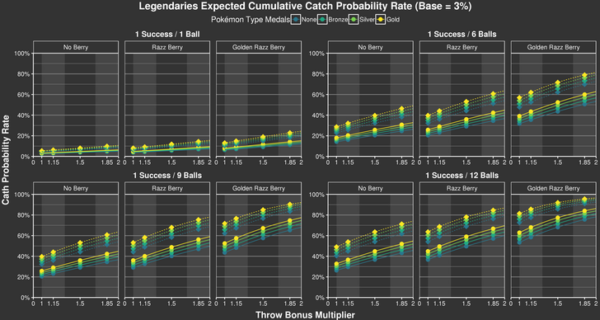
Figure 2: Combined catch probability for Pokémon with a BCR of 3 % (Source)

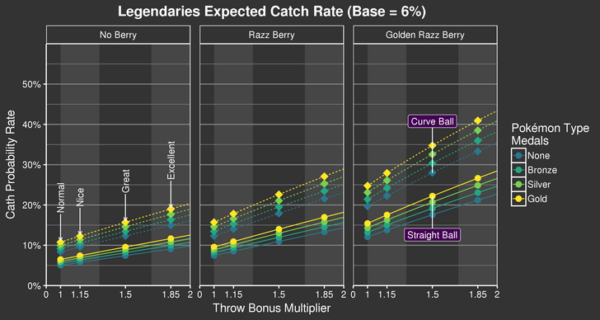
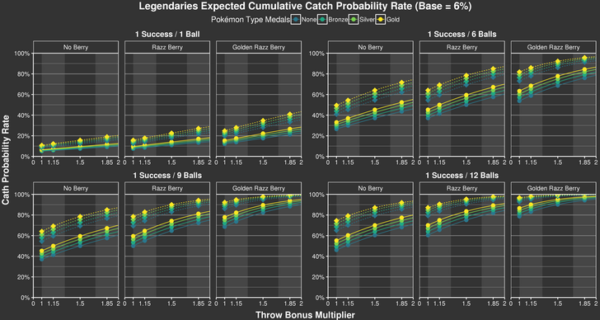
Figure 3: Combined catch probability for Pokémon with a BCR of 6 % (Source)

The difference between a straight ball and a curve ball is remarkable. A curve ball without any other bonus is almost as good as a straight excellent throw and the maximum catch probability using curve balls is around 1.5-times as high as without. If you are not throwing curve balls start practicing right now.

1.1     Catch chance for consecutive throws

Mathematically we are facing an urn problem with two different “balls” [“caught”, “broke out”]. We draw -times with replacement. The ball distribution is according to the catch chance and depends on the individual throw. The probability of catching a Pokémon after balls is therefore given by:

is the catch probability of the single throws. If every throw is identical, i.e. , we get

So, we first calculate the probability of not catching it -times and then get the opposite event.

1.2     Candy expectation value

Using the equation for the consecutive catch chance we can calculate the candy expectation value (the average amount of candy received per raid). Assuming all throws are equal, it only depends on the choice of the berries. The examples below assume an average great throw with a curve ball and transferring the Pokémon after a successful catch. All examples are made using my spreadsheet (link). Feel free to make a copy to see the results for different parameters.

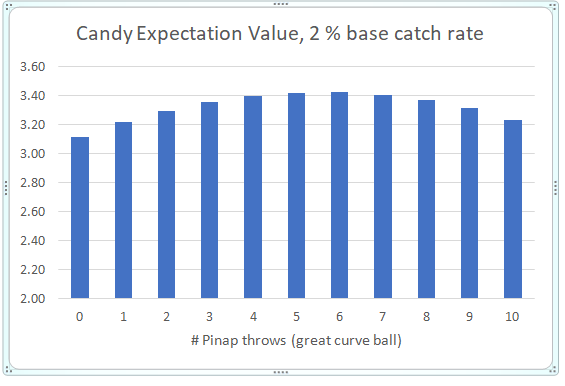
2 % base catch rate, great curve ball, Pinap Berry (6%) and Golden Razz Berry (14 %)

is the catch probability with a Pinap Berry, the number of Pinap throws. and are the catch probability and the number of Golden Razz berries respectively.

The candy expectation value is therefore given by:

and are constants for the rewarded candy with a successful Pinap or Golden Razz Berry catch respectively. Looking at the second term, we see that the expectation value depends on the order in which the berries are used. Going with Pinap first is reflected by, the chance of not catching it after Pinap throws. Using Golden Razz Berries before Pinaps reduces the chance of catching it with a Pinap Berry and therefore the expectation value as well.

Since some Pokémon (e.g. raid bosses) can be useful even at level 20, it makes sense to also include the total catch probability. So, we define a simple decision metric:

is just a constant to normalize the results. If we want to include the Pokémon’s IVs (see section 6) we could use them to weight the catch probability and the expectation value: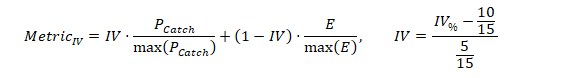

is a rescaled value of the to the interval, since raid bosses don’t have the full IV-range. One could also add another subjective weight depending on the personal preference – catching more raid bosses or getting more candy.

Pinap Berries	Golden Razz Berries	Total catch probability	Expectation value	Metric
0	10	77.9 %	3.11	0.99
1	9	75.8 %	3.21	1.00
2	8	73.6 %	3.29	1.00
3	7	71.1 %	3.35	0.99
4	6	68.4 %	3.39	0.97
5	5	65.5 %	3.42	0.94
6	4	62.3 %	3.42	0.91
7	3	58.8 %	3.40	0.86
8	2	54.9 %	3.37	0.80
9	1	50.7 %	3.31	0.74
10	0	46.1 %	3.23	0.67

Table 10: Catch probability and candy expectation value for different berry strategies (10 balls, 2 % BCR)

Pinap Berries, IV [%]	100	96.7	93.3	90.0	86.7	83.3	80.0	76.7	73.3	70.0	66.7
0	1.00	1.00	1.00	1.00	1.00	1.00	0.98	0.96	0.94	0.92	0.89
1	0.97	0.98	0.99	0.99	1.00	1.00	0.99	0.98	0.96	0.94	0.92
2	0.95	0.96	0.97	0.98	0.99	1.00	1.00	0.99	0.98	0.96	0.95
3	0.92	0.93	0.95	0.97	0.98	1.00	1.00	1.00	0.99	0.98	0.97
4	0.89	0.91	0.93	0.95	0.97	0.99	1.00	1.00	1.00	0.99	0.98
5	0.85	0.87	0.90	0.92	0.95	0.97	0.99	1.00	1.00	1.00	0.99
6	0.81	0.84	0.87	0.90	0.93	0.96	0.98	0.99	1.00	1.00	1.00
7	0.77	0.80	0.83	0.87	0.90	0.93	0.96	0.98	0.99	1.00	1.00
8	0.72	0.76	0.80	0.83	0.87	0.91	0.93	0.96	0.97	0.99	0.99
9	0.68	0.71	0.75	0.79	0.84	0.87	0.91	0.93	0.95	0.97	0.98
10	0.62	0.66	0.71	0.75	0.79	0.84	0.87	0.90	0.93	0.95	0.96

Table 11: Decision metric dependent on Pokémon’s IV (10 balls, 2 % BCR)

Figure 3: Candy expectation value depending on the number of used Pinap instead of Golden Razz Berries, 2 % BCR, 10 balls, 1st evolution (3+1 candies)

Summary:

A mixture of Pinap and Golden Razz Berries returns the highest candy expectation value. This is achieved by throwing roughly the first half of balls with Pinaps and the rest with Golden Razz Berries. The total catch probability drops from roughly 78 % to 65 % because of using some Pinaps instead of Golden Razz Berries. This strategy is mostly useful for raid bosses with bad IVs, especially if one already has a “better” one and no longer needs it for the Pokedex. In the long run, one receives around 10 % more candy at the cost of 13 % less Pokémon caught. This strategy also has the externality of saving Golden Razz Berries for the future high IV encounters when an “all-Golden Razz Berry” strategy might be more desirable to better ensure capture.

If one wants to choose a mixed strategy, the simple metric suggests throwing 1-3 Pinaps (see Table 10Table 10: Catch probability and candy expectation value for different berry strategies (10 balls, 2 % BCR)), while the advanced IV-metric recommends to start using Pinap Berries on Pokémon below 83% IVs up to a maximum of 6 throws (see Table 11). In the end, everyone must choose his/her own strategy depending on personal preferences. There is not one perfect strategy that maximizes each variable.

2 % base catch rate, great curve ball, Pinap Berry (6%) and standard Razz Berry (14 %)

Figure 4: Candy expectation value depending on the number of used Pinap instead of normal Razz Berries, 2 % BCR, 10 balls, 1st evolution (3+1 candies)

Summary:

Using normal Razz Berries instead of Golden ones, the highest expectation value is given by just throwing with Pinap Berries (see Figure 4). The total catch probability drops from around 61 % with just Razz Berries to roughly 46 % with 10 Pinap throws, while returning 30 % more candy on average.

5 % base catch rate, great curveball, Pinap Berry (6%) and Golden Razz Berry (14 %)

Here we have another example of a typical level 4 raid boss with a base catch rate of 5 % and 10 candy for a successful catch (3. evolution), i.e. Tyranitar.

Pinap Berries	Golden Razz Berries	Total catch probability	Expectation value	Metric
0	10	98.7 %	9.87	0.68
1	9	98.3 %	11.27	0.78
2	8	97.8 %	12.42	0.85
3	7	97.1 %	13.38	0.91
4	6	96.2 %	14.14	0.95
5	5	95.1 %	14.75	0.98
6	4	93.7 %	15.21	1.00
7	3	91.9 %	15.53	1.00
8	2	89.5 %	15.72	0.99
9	1	86.5 %	15.77	0.96
10	0	82.5 %	15.68	0.91

Table 12: Catch probability and candy expectation value for different berry strategies (10 balls, 5 % BCR)

Figure 5: Candy expectation value depending on the number of used Pinap instead of Golden Razz Berries, 5 % BCR, 10 balls, 3^rd evolution (10+1 candies)

Summary:

Compared to the example with 2 % base catch rate, the maximum of expected candies shifts significantly towards more Pinap throws. One should also note that the expectation value only increases by around 5 % between the first half of the balls and the maximum, while the total catch probability drops from 95 % to 85 %. If one, therefore, wishes to maximize the candy one should only use the Golden Razz Berry on the last ball.

The simple metric reflects that the expectation value barely raises after the first half of the balls and suggests throwing the second half with Golden Razz Berries. Therefore, we get a total catch probability of around 95 %, while reaching 93.5 % of the maximum candy expectation value. Throwing with 10 Golden Razz Berries leads to a total catch probability of 98.7 %, but the candy expectation value drops to 62.5 % of its maximum.

1.3     Throwing Technique

Besides the number of balls, the throwing technique has a substantial influence on the catch probability. Every missed throw has a catch probability of zero!
Therefore one should practice being able to hit great throws most of the time. One should only go for excellent throws if one really hits them reliably. The difference between a great and an excellent throw is not too big, so that sometimes missing some excellent throws in exchange for hitting some can be worse than always hitting great throws.

For a visual guide, check out the locking target trick comic (Source) (Note: The flash got removed)

Once one can reliably hit great curveballs throws, one can really profit from the following trick (details see Figure 6, video example):

1. Hold the ball until the circle gets to a size that can be hit reliably. Release the ball at the bottom of the screen (make sure not to throw it).
   Remark: If the Pokémon breaks out, the circle does not reset, so it only must be set once if all steps are performed correctly.
2. Wait patiently, until the Pokémon starts its defense animation. (Note: The flash got removed)
3. Grab the ball and start spinning it.
4. Perform 2-3 spins (1.5-2.5 s depending on the animation length and throw distance) before you release the ball. Make sure to release it before the animation has ended.
5. With a bit of training and good timing, the ball will hit the boss just after the animation has ended.

Important Note:
The ball must be released before the animation ended, otherwise, the circle size will change. Patience and timing is the key to successfully catch raid bosses. It is even possible to hit the boss between two back to back defense animations, so it is possible to hit every throw!